Difference between revisions of "Random Walk"
(started page) |
(add triangular images) |
||
| Line 13: | Line 13: | ||
Distribution: | Distribution: | ||
| + | |||
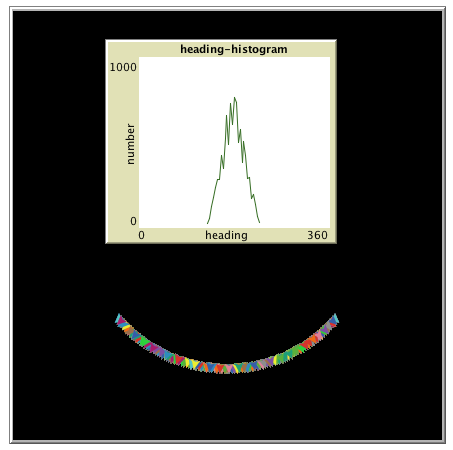
| + | [[File: triangular_heading.png]] [[File: triangular_walk.png]] | ||
=Some Theory= | =Some Theory= | ||
Revision as of 18:44, 6 October 2019
Random Walks in NetLogo
rt random 360 fd 1
Triangular Random Walk
Advance +/- 50 degrees from straight ahead, gives a triangular distribution around 0
rt random 50 lt random 50
Distribution:
Some Theory
In a true random walk (ie Brownian motion) the mean displacement along the x-axis is proportional to the square root of time dx=sqrt (2Dt), which gives mean radius of a circle covered by the random walk
Einstein, Albert (May 1905). "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen" (PDF). Annalen der Physik (in German). 322 (8): 549–560. Bibcode:1905AnP...322..549E. doi:10.1002/andp.19053220806. Retrieved 2008-04-10.
Einstein, Albert (1989). "On the movement of small particles suspended in a stationary liquid demanded by the molecular-kinetic theory of heat" (PDF). Princeton University Press
A random walk constrained on a lattice:
McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.