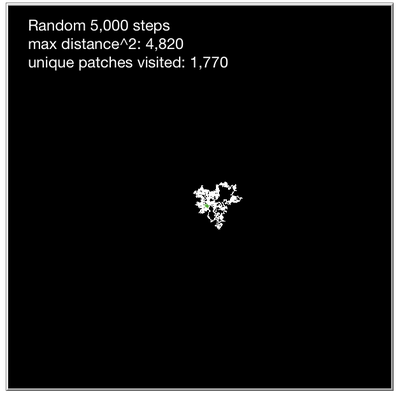
Random Walk
Random Walks in NetLogo
Each tick, generate a random heading from 0-359. Gives an even distribution of headings, and the resulting random walk has lots of backtracing and crossings.
rt random 360 fd 1
Triangular Random Walk
Advance +/- 50 degrees from straight ahead, gives a triangular distribution around 0. As a result, the turtles have a much greater tendency t move forward, and so cover a wider range and show less backtracing and crossing (and visit more unique patches).
rt random 50 lt random 50
Distribution:
Some Theory
In a true random walk (ie Brownian motion) the mean displacement along the x-axis is proportional to the square root of time dx=sqrt (2Dt), where D is the diffusion constant which gives mean radius of a circle covered by the random walk
Einstein, Albert (May 1905). "Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen" (PDF). Annalen der Physik (in German). 322 (8): 549–560. Bibcode:1905AnP...322..549E. doi:10.1002/andp.19053220806. Retrieved 2008-04-10.
Einstein, Albert (1989). "On the movement of small particles suspended in a stationary liquid demanded by the molecular-kinetic theory of heat" (PDF). Princeton University Press
A random walk constrained to 2 dimensions, the mean displacement is proportional to sqrt(t).
There are supposed to be interesting properties of random walk on a lattice, which is probably the best model of NetLogo movement.
McCrea, W. H. and Whipple, F. J. W. "Random Paths in Two and Three Dimensions." Proc. Roy. Soc. Edinburgh 60, 281-298, 1940.